Deze tekst is gebaseerd op het artikel dat in het juni nummer (nr 7) 2012 van Euclides, vakblad voor de wiskundeleraar is geplaatst.
Perzische mozaïeken ontwerpen in de klas
Leerlingen in het centrum van een middeleeuwse ontwerptraditie
Een serie lessen waarin de leerlingen de rol aannemen van een middeleeuwse Perzische mozaïekontwerper en uiteindelijk zelf een origineel mozaïek maken, analyseren en presenteren. Is dat nog wel wisk

Inleiding
Islamitische mozaïeken vormen een interessante categorie uit alle typen geometrische betegelingen van het platte vlak. Ze zijn sinds de achtste eeuw ontworpen en uitgevoerd op tal van religieuze bouwwerken en pleinen en ook gebruikt als decoratie van manuscripten. De meetkundig meest intrigerende ontwerpen zijn rond de 12e tot 16e eeuw gerealiseerd in tegelwerk. Prachtige uitvoeringen zijn te vinden in het Alhambra in Granada (Spanje), in Fez (Marokko), op moskeeën in Isfahan (Iran) en in Samarkand (Oezbekistan), maar ook op talloze andere locaties.
Een mooie toepassing van meetkunde
De in pastelkleuren uitgevoerde mozaïeken, vaak gecombineerd met bloemmotieven of teksten in sierlijke kalligrafie of juist strak en hoekig kufi, herbergen een schat aan meetkundige didactische toepassingen. Ze kunnen bestudeerd worden vanuit veel verschillende wiskundige invalshoeken waarbij vragen kunnen worden gesteld als: Welke symmetrieën herbergen ze? Welke hoeken komen er in voor en zou je die ook nauwkeurig kunnen berekenen? Hoe zijn de verhoudingen tussen oppervlaktes van de verschillende tegels? Uitgaande van bepaalde patronen is ook bijvoorbeeld de stelling van Pythagoras te bewijzen. Al deze invalshoeken sluiten goed aan bij de huidige wiskunde in het voortgezet onderwijs op elk niveau. Dan gaat het om onderwerpen als: Leren werken met de kompasroos en geodriehoek, rekenen met hoeken, spiegel- en rotatiesymmetrie, goniometrie vanaf klas 2 en 3, voortgezet bij wiskunde B op havo en vwo tot aan het geven van meetkundige bewijzen op vwo.
Een enkele keer komt men bij deze onderwerpen vlakvullingen als voorbeeld tegen. Bijna nooit wordt het verband met islamitische mozaïeken gelegd. Een voor de hand liggende kans om een rijk stukje cultuurgeschiedenis met wiskunde in verband te brengen wordt daardoor gemist. Het zou nuttig zijn als hier meer mee gedaan werd in het wiskunde onderwijs, zeker nu een behoorlijk deel van de Nederlandse jeugd een islamitische achtergrond heeft. Daarbij komt dat het kunstzinnige element heel veel jongeren inspireert, wat een positieve uitwerking kan hebben op de interesse in het vak wiskunde.
Islamitische mozaïeken als centraal thema
Hier ga ik niet verder in op de vraag hoe men mozaïeken als voorbeeld bij de bovengenoemde meetkundige onderwerpen zou kunnen gebruiken. Één van de belangrijkste doelen van mijn onderzoek was namelijk het ontwerpen van een op zichzelf staande lesserie (lengte acht tot twaalf lessen, 15 tot 20 uur studie) voor leerlingen vwo uit het Cultuur en Maatschappij profiel (Wiskunde C) die ook geschikt is als keuzeonderwerp bij wiskunde A . Daardoor kon veel radicaler gekozen worden voor islamitische mozaïeken als centraal wiskundig thema, niet als illustratie bij andere wiskundige onderwerpen. Ook kon ik kiezen voor een interessante centrale vraag:
Hoe ontwierp men destijds de vaak zeer complexe vlakverdelingen?
Deze vraag is moeilijk te beantwoorden. Er zijn talloze uitvoeringen van ontwerpen op gebouwen te vinden, maar als het gaat om originele ontwerptekeningen zijn de bronnen schaars. Daarbij komt dat deze tekeningen meestal geen begeleidende tekst hebben. Is die er wel, dan gaat het alleen om instructies hoe het mozaïek op de gewenste schaal kan worden getekend. Deze instructies zeggen vaak maar weinig over het ontwerpproces. Wat wel blijkt uit één van de bronnen is, dat er destijds bijeenkomsten werden georganiseerd waar zowel mozaïekontwerpers als de zuiver wiskundig beter geschoolden (denk bijvoorbeeld aan astronomen/astrologen) aan deelnamen. Tijdens zulke bijeenkomsten werden meetkundige vraagstukken besproken zoals: Hoe construeer ik een regelmatige vijfhoek met passer en liniaal?
Deze informatie bracht me op het idee om de leerlingen in de lesserie te laten kennismaken met de islamitische ontwerptraditie door hen zelf nieuwe mozaïeken te laten ontwerpen. Door de leerlingen de rol van middeleeuws ontwerper te laten spelen zouden ze vanzelf geconfronteerd worden met meetkundige vraagstukken en kunnen ontdekken hoe de ontwerpers destijds zouden kunnen hebben gewerkt. De historische en creatieve context die zo ontstaat, maakt de lesserie zeer geschikt voor de doelgroep.

Opzet van de lesserie
Om ervoor te zorgen dat de leerlingen zich kunnen verplaatsen in de rol van een middeleeuwse mozaïekontwerper moeten ze eerst kennismaken met bestaande mozaïeken en een aantal ontwerp-vaardigheden onder de knie krijgen. De beschikbare tijd hiervoor is beperkt. Daarom ontwikkelde ik een toegankelijke methode om islamitische mozaïeken te analyseren. De behandeling van deze analysemethode vergt ongeveer vier lessen en bereidt de leerlingen voor op de fase waarin vaardigheden voor het zelf ontwerpen worden aangeleerd. Bij deze fase moest de keuze worden ingeperkt. Ik koos ervoor in te zoomen op de Perzische ontwerpmethode met behulp van het zogenaamde basispatroon, om een viertal redenen: Omdat hierover uit enkele primaire bronnen en indirect, via secundaire bronnen voldoende informatie is te achterhalen, omdat deze methode in de zestiende eeuw geleid heeft tot vele prachtige, fascinerende resultaten, omdat er interessante toegepaste wiskunde bij komt kijken en omdat met deze methode in relatief korte tijd mooie, unieke ontwerpen te maken zijn.
Ik geef hieronder een kort overzicht van de analysemethode die de leerlingen hanteren. Daarna volgt een uiteenzetting van de vaardigheden die worden aangeleerd om een Perzisch mozaïek zelf te kunnen ontwerpen. In de praktijk gaan deze zaken hand in hand: Door te analyseren ontdekken leerlingen methodes om te ontwerpen, en door vaardigheden te oefenen herkennen leerlingen kenmerken uit bestaande mozaïeken gemakkelijker zodat ze die beter kunnen analyseren.
Analyseren van mozaïeken
De analysemethode wordt hier uiteengezet aan de hand van het relatief eenvoudige mozaïek van figuur 3 (zie de fotogalerij hieronder).
Spiegelsymmetrieën
In figuur 4 zijn de symmetrieassen getekend. Omdat het mozaïek denkbeeldig oneindig doorloopt zijn er ook spiegelsymmetrieën langs lijnen die niet door het centrum van de figuur lopen en samen een nieuw, eenvoudig patroon vormen. (In dit voorbeeld een patroon opgebouwd uit geodriehoeken.) Dit is voor de meeste leerlingen een nieuw fenomeen dat om enige oefening vraagt.
Het begrip locale symmetrie
Figuur 5 laat de rotatiesymmetrieën zien, ook de locale rotatiesymmetrieën. Bij de rotatiecentra wordt het soort rotatiesymmetrie aangegeven: T4 betekent bijvoorbeeld dat het gehele patroon een viervoudige rotatiesymmetrie heeft rond het aangegeven centrum (T staat voor ‘Totaal’). L8 betekent dat er een achtvoudige rotatiesymmetrie is die echter niet geldig is voor het gehele patroon, maar enkel locaal; binnen de aangegeven cirkel. Het begrip locale symmetrie wordt geïntroduceerd omdat dit een kenmerkende eigenschap is van vele islamitische mozaïeken.
De begrippen cel en kleinste cel
Vrijwel elk islamitisch mozaïek heeft een zichzelf herhalende cel. Er wordt onderscheid gemaakt tussen een kleinste cel en een cel. Deze laatste is bij voorkeur rechthoekig en wordt in de weinige manuscripten die we kennen veel aangetroffen. De afmetingen van een cel hangen nauw samen met de translatiesymmetrieën van het patroon. Een kleinste cel is een zo klein mogelijk gebiedje uit het mozaïek waarmee door middel van spiegelen en schuiven het gehele mozaïek kan worden opgebouwd. Het is vaak opmerkelijk hoe weinig er slechts hoeft te worden getekend om vervolgens daarmee, door middel van lineaire transformaties het gehele mozaïek op te bouwen. Zie figuur 6.
Leerlingen worden uitgedaagd om in bestaande mozaïeken een cel en een kleinste cel te identificeren. De symmetrieassen zijn hierbij vaak een leidraad omdat het
handig is om de cel zo te kiezen dat enkele daarvan langs de rand van de cel lopen.
Een Perzische ontwerpmethode: Basispatronen
Veel Perzische mozaïeken zijn ontworpen met behulp van een basispatroon. Dit basispatroon is een hulpmiddel bij het ontwerpen en is in het uitgevoerde mozaïek niet meer zichtbaar. Het is een patroon dat is opgebouwd uit veelhoeken met gelijke zijden. In de moderne literatuur worden deze veelhoeken vaak Girihtegels genoemd (naar het Perzische woord girih, knoop). Vaak is er ten minste één type regelmatige veelhoek gebruikt. In de regelmatige veelhoeken worden vervolgens sterren geplaatst, en wel zodanig, dat de sterpunten samenvallen met de middens van de zijden van de veelhoek. Het mozaïek van figuur 3 heeft ook een basispatroon, zie figuur 7 (laatste tekening van de galerij boven). Dit basispatroon bestaat uit drie soorten girihtegels; een regelmatige achthoek, een vierkant en een zeshoek in de vorm van een strikje. In de regelmatige veelhoeken zijn sterren geplaatst en door de lijnen bij de sterpunten te verlengen ontstaan in de strikjes vliegers die in vorm en grootte die van de vliegers in de regelmatige achthoeken benaderen. Zo ontstaat een evenwichtig mozaïek.

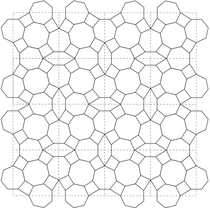
Soms leidt het plaatsen van sterren in een basispatroon echter niet tot een erg evenwichtig mozaïek. Zie bijvoorbeeld figuur 8 boven, waarbij ik in een ander basispatroon in de regelmatige veelhoeken sterren heb geplaatst. De strikvormige girihtegels zijn dan echter lastig in te vullen op een wijze die goed aansluit bij de rest van het mozaïek. Plaatsing van rozetten in plaats van sterren in de regelmatige veelhoeken blijkt hier tot een mooier resultaat te leiden. Dit is door middeleeuwse Perzische ontwerpers toegepast, zie figuur 1. De lezer wordt uitgenodigd het onderliggende basispatroon van dit mozaïek zelf te achterhalen.

Sterren en rozetten
Omdat niet alleen sterren, maar ook rozetten vaak worden gebruikt in Perzische mozaïeken leert de leerling een eenvoudige typologie van rozetten. Ik maak onderscheid tussen drie typen rozetten, zie figuur 9. (D8 verwijst naar de achtvoudige draaisymmetrie; de twee hoeken verwijzen naar twee kenmerkende hoeken van het rozet.)
Veel rozetten uit Perzische mozaïeken hebben bepaalde extra eigenschappen die bijdragen aan een evenwichtig eindresultaat. Deze rozetten noem ik standaardrozetten. De kenmerken van een standaardrozet worden uiteengezet in figuur 10. In de lesserie wordt behandeld hoe een standaardrozet met gebruik van passer en liniaal kan worden geconstrueerd.
Uiteraard zijn er nog vele andere typen rozetten die in de Perzische ontwerptraditie en elders voorkomen. De beperking tot deze groep volstaat echter om bij de ontwerpfase tot mooie resultaten te kunnen komen.

Deze figuur laat drie type-1-rozetten in een pentagon zien die voldoen aan de eisen voor een standaardrozet (SR): Volgens de eis voor lengtes van zijden moet daarvoor gelden: DA = DC en AB = BC (zie figuur links). Hieruit volgt dat de som van een naar buiten wijzende hoek van een zeshoek en van een punt van de centrale ster 180º is (figuur midden: 108 +72 = 180º, figuur rechts: 144 + 36 = 180º. In de linker figuur zijn beide hoeken 90º). Een standaardrozet van een zeker type in een regelmatige veelhoek heeft dus slechts één vrijheidsgraad.

Mozaïeken ontwerpen en presenteren
Nadat leerlingen verschillende mozaïeken hebben geanalyseerd, hebben kennisgemaakt met het begrip ‘basispatroon’ en geoefend hebben met het tekenen van sterren en rozetten in regelmatige veelhoeken, gaan ze in groepjes aan de slag met het ontwerpen van een nieuw mozaïek. Ze maken eerst een basispatroon. Vervolgens worden geschikte sterren of rozetten in de regelmatige veelhoeken getekend. Ten slotte krijgen de veelhoeken die niet regelmatig zijn een bijpassende invulling. Om een aantrekkelijk eindresultaat te kunnen presenteren wordt per groepje een gekleurd mozaïek, eventueel met een passende randversiering, extra bloemmotieven of een gekalligrafeerde tekst op posterformaat gemaakt. Deze wordt samen met een poster met uitleg over het ontwerpproces en een analyse getoond in een korte eindpresentatie voor de klas of tijdens een presentatieavond voor een groter publiek. Het eindresultaat wordt beoordeeld door de docent of door een vooraf vastgestelde jury.

Ervaringen uit de lespraktijk
De lesserie is tot heden in vier klassen gedaan; tweemaal in een vierde klas VWO wiskunde A in Rotterdam, door leerlingen met een veelal islamitische achtergrond en tweemaal door een vijfde klas VWO wiskunde A/C op Texel door leerlingen die bijna allemaal geen affiniteit hadden met de islam.
In alle klassen werd met goede inzet aan de opdrachten gewerkt. Op beide scholen werd de cursus in het tweede jaar als praktische opdracht opgenomen in het PTA. Uit enquêtes achteraf aan de leerlingen bleek dat men de moeilijkheidsgraad van de lesserie gemiddeld normaal tot iets te moeilijk vond. Verder bleek dat men het idee had dat er iets minder wiskunde werd geleerd dan tijdens reguliere wiskundelessen, maar dat er meer algemene kennis werd verworven. Dit komt wellicht door het feit dat men zich vaak niet realiseert dat het gehele ontwerpproces een voornamelijk wiskundige activiteit is waarbij het gaat om een vorm van wiskunde die men niet zo gewend is. De opzet met eindpresentaties werkte goed; deze werden veelal met enthousiasme gegeven en er werd veel inzet getoond bij het maken van de posters. Hierbij was er geen merkbaar verschil tussen de houding van leerlingen met, en leerlingen zonder een islamitische achtergrond.
Door deze lesserie te doen hebben leerlingen niet alleen veel opgestoken over onderwerpen als geometrie, symmetrie en toegepaste wiskunde, maar ook over de culturele en historische achtergrond van geometrie en verbanden met architectuur in de islamitische cultuur. Door de focus op de wiskundige inhoud is de islamitische ontwerptraditie van geometrische mozaïeken zeer goed bruikbaar in de wiskundeles voor elke leerling, wat zijn of haar culturele achtergrond ook is. Een breder gebruik ervan zou een verrijking zijn voor het wiskunde onderwijs in Nederland.
Literatuur
Op www.patterninislamicart.com is een groot archief foto’s van islamitische mozaïeken te vinden. Zie ook de links op deze site.
Prof. J.P. Hogendijk heeft veel gepubliceerd over dit onderwerp. Zie www.jphogendijk.nl .

Over de auteur: Goossen Karssenberg was ruim twintig jaar werkzaam als docent wiskunde in het middelbaar onderwijs. In de jaren 2009-2011 was hij tevens als LIO (Leraar In Onderzoek, gefaciliteerd door NWO) verbonden aan de Universiteit Utrecht (Geschiedenis van de wiskunde, Freudenthal Instituut). Van zijn onderzoek is onder meer dit artikel het resultaat. Thans schrijft hij onder andere lesmateriaal, geeft hij workshops en lezingen over islamitische mozaïeken en maakt in samenwerking met beeldend kunstenaar Maria Roelofsen kunstvoorwerpen waarin hij mozaïeken verwerkt.
 José Goossen Karssenberg Islamitische Meetkundige Patronen
José Goossen Karssenberg Islamitische Meetkundige Patronen