José Goossen Karssenberg Islamitische Meetkundige Patronen
Een aperiodieke monotegel
Na een halve eeuw is het eindelijk gelukt: De tegelset van twee van Roger Penrose is nu gereduceerd tot een set van één!
David Smith, Joseph Samuel Myers, Craig S. Kaplan en Chaim Goodman-Strauss vonden deze 'monotile', ook wel 'einstein' genoemd, en publiceerden hierover in maart 2023.
Eigenlijk is het een familie van tegels die allemaal een einstein zijn. De onderstaande tekening is er eentje van, deze past keurig op een isometrisch grid en bestaat uit acht vliegervormen, hieronder met gele lijnen aangegeven. Deze heeft de naam 'hoed' gekregen.
Zoals je ziet heb ik in blauw een patroon ontworpen, geïnspireerd op de islamitische ontwerptraditie.
Hier kan ook vlechtwerk op toegepast worden. Omdat ook de 'onderkant' van de tegel gebruikt wordt (je mag de tegel dus omkeren bij het puzzelen), krijgt die dan ook een eigen vlechtwerkinvulling:
Met deze twee tekeningen kun je een aperiodiek patroon met vlechtwerk maken.
Bovenstaande tegel behoort tot dezelfde familie. Deze heeft allemaal even lange zijden behalve eentje die dubbel zo lang is. Zoals je ziet is die opgebouwd uit een strikvorm en een klaver-drie-vorm. Beide zijn heel bekend in de islamitische ontwerptraditie.
Hieronder zie je dezelfde vorm, maar dan met rode en blauwe zijden. Hiermee kun je afleiden hoe de hele familie einsteins eruitziet: je kunt bijvoorbeeld alle rode zijden korter of langer maken, als ze maar even lang blijven, alle zo gevormde tegels vormen een einstein.
Behalve nu juist de tegel waarbij de rode en blauwe even lang zijn, want daarmee kun je het vlak ook periodiek betegelen. Houd je je echter aan de regel dat rood op rood, en blauw op blauw moet uitkomen, dan is dit ook een einstein.
Wil je een aperiodieke betegeling maken, dan mag je dus niet twee tegels tegen elkaar aan leggen zoals hieronder:
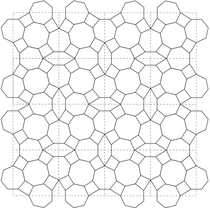
Een stukje aperiodieke betegeling met de 'klaverstrik' (zo noem ik deze tegel omdat die is te verdelen in een klaver- en een strikvorm, zie linksonder) ziet er dan zo uit, waarbij alleen de blauwe tegel ondersteboven is gelegd (met andere woorden, dit is de gespiegelde vorm):
Deze tegelvorm biedt enorm veel mogelijkheden om nieuwe aperiodieke islamitische patronen te maken. Op zowel de strikvorm als de klavervorm kun je namelijk heel mooie patronen ontwerpen. Dit heb ik al eens gedaan om periodieke patronen te reconstrueren (bijvoorbeeld het patroon met zevensterren uit Samarkand) of nieuwe te ontwerpen.
Dus hopelijk later meer!
Recent Activities, News
Workshopdagen Valuascollege Venlo juni 2024
Klik op de foto naar een verslag
Houten versie Geofractor
De plastic geofractor uit het boekje is nu ook verkrijgbaar in de houten variant. Prijs €12,50
Boekje in zebrareeks is half april 2023 verschenen.
Artikel in Euclides
Half maart 2023 is in het vakblad van wiskundeleraren een artikel van me verschenen naar aanleiding van de publicatie van Zebra 66 Islamitische Meetkundige Patronen
Recensie Snijpunt Isfahan
Lees hier
First prototype of new aperiodic puzzle
The developing process is continued. click here.
Ars et Mathesisdag 2019
During the art- and maths day (Ars et Mathesisdag), 24 november 2018, I gave a lecture about analyzing historical geometric patterns and trying to find new ones.
Timelapse construction
A great timelapse construction by Ameet Hindocha. More can be found on the website Ambigraph
Article online available
The journal For the Learning of Mathematics made my 2014 article 'Learning geometry by designing Persian mosaics' online available: See https://flm-journal.org/Articles/2E0CB6E94D76C79C2F341680D60F17.pdf
Een kritische recensie van Snijpunt Isfahan
Here you find my reflections on a very critical review of Snijpunt Isfahan by a mathematician (in Dutch)
March 30 2018 Lecture
Lecture in Dutch
Two new 'floral'patterns
24 March 2018
Based upon the famous Alhambra pattern with circle segments. Click on the picture below to go there
14 feb 2018 Event about 'Snijpunt Isfahan' at Spui25
Look here
Interview by Dolf Jansen
Dolf Jansen interviewed Maite and me (in Dutch) during the radio program 'Spijkers met Koppen', to hear and watch the interview, klick here
Interview by Coen Verbraak
Coen Verbraak interviewed Maite and me about Maite's book 'Snijpunt Isfahan' (in Dutch), to hear and watch the interview, klick here
Official opening of Museum Gallery RAT (Recomposed Art Texel)
May 13 2017 we celebrated the opening of our new location Burgwal 20 Den Burg. Here you find artwork composed with beachcombed materials by Maria Roelofsen and my design studio for making new pattern compositions based upon the Islamic design tradition. For further information also look at www.museumgalerierat.nl
A new floral design with worksheet. Click on the picture to find more information about the Khatai Flower.
March 24th 2017
Heart cloud sun
Workshop in Amsterdam
21 august 2016 11.30-13.00
In the Tropenmuseum I delivered a workshop on the Islamic design tradition of geometric patterns in Dutch, further information here
Floral designs
A new subject is being developed and information will be available on this website: floral designs. I started today with the lotus flower. Click on the lotus below to visit the right tab.
24th of March 2016
Colour Plates available (not any more since the exhibition ended)
Download my puzzle-/colour plates at this link of the Tropenmuseum Junior
Short story 'Spiral Figures'
I wrote a short story in Dutch about a child who draws spiral figures at the beach
Students finished newly developed lesson strand on Islamic mosaic design
Click on the picture below and check the two slide shows on the 2015 results.
The workshop I delivered in 2014 is online since Jan. 2015
A miraculous set of tiles
Patchwork by Marijke Maris-Baan
Heptagon construction
A method to construct a near-regular heptagon now published on this site
Result of drawing competition
6 July 2014. The drawing cmpetition was won by José Bradamonte.
Students finished mosaic design course
A group of about 20 students finished the lesson strand on Persian style mosaics in the beginning of may 2014. You can find some impressions of their activities here
View their endresults here
Result of pre-study
Article published
2014, March.
My article 'Learning Geometry by Designing Persian Mosaics' is published in issue nr. 100 (March 2014) of the Canadian journal 'For the Learning of Mathematics'.
At the flm-website you can find an Abstract.
Examples of basic patterns
New pattern design
Click on the picture below to find a series of patterns with octagons
Workshop 1&2 Feb. 2014
The workshop held on Texel was attended by 13 people in total. Among them: a furniture maker, a designer of lamps, quilters, painters and teachers. See the photo-impression of the workshop
Article in local newspaper Texel
This article (text and photo Pip Barnard) is about my fascination for Islamic geometrical ornamentation and how it can be used in (mathematics) education.
Article in Dutch newspaper
An article about the artwork by Maria Roelofsen and myself was published in the Dutch newspaper 'Reformatorisch Dagblad' on 30 december 2013. (Text Janneke van Reenen-Hak, Photo's Sjaak Verboom)
Publication in dutch magazine 'Experiment NL'
In this magazine on dutch Scientific research an article was published about my work. All those who have a subscription of 'Quest' received this magazine. Four pages with beautiful illustrations!
International workshop on Islamic geometric design Istanbul
At the Design Center of Istanbul a six-days congres was organized with lectures and workshops delivered by experts in this field. Incredibly inspiring!
Conference Isfahan, Iran
May 2013. A three day conference for mathematicians and artists on geometric Islamic patterns was held. Lots of inspiring workshops and lectures were delivered.
Workshop Leiden
Workshop for students, Institute for Studies of the Middle East, Leiden University, 27 march 2013
Contribution to piece of art
Lecture for maths teachers
During the conference for Maths teachers held december 18th 2012 at the Groningen University I gave a lecture about using islamic mosaics to teach geometry at all levels in secundary schools.
Article Published
June 2012.
In the review for Dutch mathematics teachers called 'Euclides' the article 'Designing Persian Mosaics in the Classroom. Students in the centre of a medieval design tradition' appeared (for the article in Dutch click here).
Maria completed 'the frog'
