Mozaïek met vierpuntige sterren en zeshoeken - Goossens geometric pattern website
Het vierster-zeshoekpatroon
Twaalf verschillende reconstructies van één patroon

Het tableau aan de onderzijde, omkaderd met een groene rechthoek is opgebouwd uit twee elementen: een vierpuntige ster en een zeshoek.
Het patroon is op veel manieren te reconstrueren, ik laat hier alle methodes zien, om te beginnen een paar makkelijke manieren met vouwblaadjes, daarna de serieuzere manieren. tot slot laat ik varianten zien en verbanden met andere patronen.
Wat blijkt is, dat je enorm veel kunt leren van de studie van één enkel, eenvoudig patroon.
Foto Manuel Martínez Vela,
uit het Alcázar, Sevilla

Dit is een detail van een metalen deur met deurknop uit het Mezquita, Cordaba waarop hetzelfde patroon te zien is.
Foto Paul Barchilon.
De decoratie van het patroon heeft een schildvorm met daarin een kruis. Bewijs dat het is gemaakt nadat het Kalifaat van Córdoba rond 1035 was uiteengevallen en het gebied was veroverd door katholieke Spanjaarden
1 De zeshoek maken met een vierkant vouwblaadje
2 De ster maken met vier vierkante vouwblaadjes

Voer vier keer de eerste stap van methode 1 uit om de juiste stervorm te maken. Maak meerdere van deze sterren uit vier vliegervormen en stel hiermee het patroon samen.
3 De ster maken met één vierkant vouwblaadje
4 Een 'kleinste cel' vouwen met een vierkant vouwblaadje

Gebruik een vierkant vouwblaadje ABCD. Vouw alle grijze lijnen, begin met de twee diagonalen. De blauwe lijnen vormen het patroon.
Maak dus meerdere van deze kleinste cellen en leg ze tegen elkaar, bedenk dat de punten B en D viervoudige rotatiepunten van het patroon zijn en de punten A en C tweevoudige.
Een uitleg over waarom je hiermee het patroon kunt leggen vind je in het intermezzo hieronder

Intermezzo: Een analyse van het patroon


Op de bovenstaande foto zijn in blauw twee vierkanten aangegeven die samen een zogenaamde 'cel' vormen. Hiermee kun je het hele mozaïek als het ware stempelen.
Je kunt ook een kleinere vorm kiezen waarmee het hele patroon te stempelen is, bijvoorbeeld het rode vierkant.
Die is in de analysetekening hiernaast uitgelicht. Rotatiesymmetrieën zijn aangegeven, evenals spiegelsymmetrie met een streepjeslijn en lokale spiegelsymmetrieën met stippeltjeslijnen.
De gele pijlen hierboven geven de translatiesymmetrieën weer.Het witte pentagon in de foto hierboven is trouwens ook een kleinste cel
5 Een halve cel vouwen met een vierkant blaadje
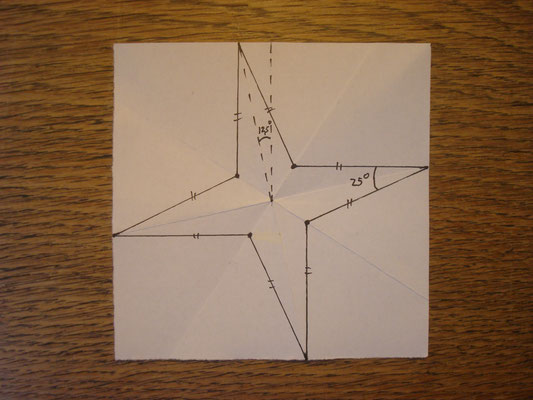
Dit is een vouwinstructie waarbij je met de geodriehoek een scheef kruis vouwt om de constructie van de ster in één van de blauwe vierkanten van de foto hierboven te maken.
Kies een hoek van 22,5 graden om het patroon te reproduceren. Maar je kunt ook een andere hoek kiezen. Dan krijg je een patroon met stompere of scherpere sterpunten, zie de laatste drie foto's van de serie. Voor de samenstelling van het mozaïek heb je zowel de voorkant als de achterkant (de gespiegelde ster) van het vouwblaadje nodig.
6 Een andere kleinste cel (pentagon!) vouwen uit een A-4-tje

7 het patroon tekenen op ruitjespapier

Je kunt het patroon niet exact reconstrueren met ruitjespapier. Dat komt doordat de wortel uit het getal twee irrationeel is. De tekening links is wel aardig nauwkeurig. De benadering komt neer op een afronding van wortel twee op 1,4. De zijden van het rode vierkant in de vierpuntige ster staan bijna loodrecht op de diagonalen van de ster, maar niet exact.
In het rechter patroon zijn de sterren wel spiegelsymmetrisch, maar de sterpunten zijn niet 45 graden. Ik heb hier een zogenaamd Pythagorastriplet gebruikt (de 3-4-5-driehoek)
8 Een kleinste cel construeren met passer en liniaal

Teken eerst vierkant ABCD. Teken diagonaal AC. Trek de rode cirkel om punt E te vinden. Trek de groene cirkel met middelpunt E om F en G te vinden. Trek de oranje cirkels met middelpunten B en D om H en I te vinden.
9 Een andere kleinste cel construeren (pentagon)
Deze aanpak lijkt op methode 6, maar nu met passer en liniaal in plaats van met vouwen.

Trek een horizontale en verticale lijn, Gebruik het snijpunt als middelpunt van een grote cirkel (rood).
Construeer twee bissectrices en vervolgens nog eens twee.
Met de goudgele halve cirkels vind je twee hoekpunten, links en rechts van het goudgele pentagon. Dit is een kleinste cel van het patroon.
De blauwe lijnen zijn vervolgens makkelijk te construeren.
10 Een groter veld construeren met passer en liniaal

Deze constructie lijkt op methode 8, alleen maak je nu in één keer een groter veld van het patroon. Begin met een groot vierkant. De rest spreekt voor zich.
11 Het patroon afleiden uit een veld pentagons

De goudgele lijnen vormen een veld van acht kleinste cellen van het patroon dat is te construeren met behulp van de grijze lijnen en cirkels.
Vervolgens kunnen zonder veel moeite de blauwe zeshoeken worden ingetekend en zo ontstaat het patroon.
12 het patroon maken met behulp van golvende stroken

Als je een aantal van de bovenstaande golvende stroken maakt, dan kun je het patroon ook samenstellen. De kleine rondjes verwijzen naar een uitvoering van het mozaïek in Granada, zie de foto hieronder


Dit is een resultaat met blauwe en rode gevlochten golfstroken. Wat opvalt is, dat de stroken op de plek waar ze onder elkaar doorgaan ook een bocht maken.
Dat kun je zien als een makke van het patroon, in de meeste islamitische ontwerpen wordt dit vermeden.
Varianten van het patroon

Dit mozaïek uit het Alhambra heeft zeshoeken met kleine driehoekige uitstulpinkjes. Hierdoor worden de 'bochten' bij de 'kruispunten' vermeden, maar nadeel is weer dat de vierpuntige sterren, met afgeknotte punten, niet meer symmetrisch zijn.

Ik vond deze variant van het patroon, zowel links als rechts gaf ik de zeshoeken kleine huisjesvormige 'uitstulpinkjes'. Nu blijven de sterren wel spiegelsymmetrisch. Wanneer je beide patronen laat overlappen ontstaat een nieuw patroon met achtpuntige sterren (zie het midden van de tekening).

Met leerlingen van het Cosmicus College maakte ik in 2010 dit mozaïek met variërende sterpunthoeken. Verschillende leerlingen kozen verschillende hoeken bij methode 5.
 José Goossen Karssenberg Islamitische Meetkundige Patronen
José Goossen Karssenberg Islamitische Meetkundige Patronen