Snijpunt Isfahan - Maite Karssenberg
Eind januari 2018 verscheen Snijpunt Isfahan (Uitgeverij Querido Fosfor, verkrijgbaar bij Museum Galerie RAT), geschreven door Maite Karssenberg. Het is een verslag van de reis die zij met mij maakte naar Isfahan met een bijzonder doel.
Hieronder geef ik extra informatie over de tekeningen uit het boek. Ook becommentarieer ik enkele passages uit Snijpunt Isfahan.
p.17: Het nieuwe patroon

Dit is het patroon dat ik 'op mijn zolderkamer' (p.15) bedacht heb, en ook op het omslag is afgedrukt. Het ontwerp kwam in drie stappen tot stand:
1- Keuze voor een isometrisch grid of raster (de stippellijnen in de tekening), waarbij in het ontwerp de zesvoudige symmetrieën gebroken worden, maar niet de drievoudige. Dit betekent dat het ontwerp in één gelijkzijdige driehoek drievoudig draaisymmetrisch is en dat de patronen in twee aangrenzende driehoeken elkaars gespiegelde zijn. Daarmee is één van de 17 behanggroepen (volgens de groepentheorie, waar Mohammad naar verwijst op p.85) vastgelegd.
2- De keuze van lokale symmetrieën in elke driehoek uit het raster. Die worden bepaald door de dunne doorgetrokken lijntjes in de twee driehoeken die in de tekening op de bovenste helft als een soort spinnenweb te zien zijn.
Hier ontstaat de zevenvoudige symmetrie; de middelste cirkel is verdeeld in veertien exact evengrote sectoren.
3- Het ontwerp van het patroon op dit web. Hierbij komen de regels van het ontwerpspel kijken waarover verderop meer informatie.
p.27 Het patroon uit het Museum of the Islamic Period, Teheran

De dunne lijnen tonen de zogenaamde Girihtegels. In dit ontwerp zijn dat regelmatige zevenhoeken gecombineerd met achthoekige strikvormen. In de zevenhoeken zijn zevenvoudige rozetten geconstrueerd: In het centrum zevenpuntige sterren met hieromheen zeven strikvormige blaadjes. Hierbij is gebruik gemaakt van de 'middelpuntregel'; lijnen van het patroon snijden elkaar op de middens van de zijden van de girihtegels.
De bovenste helft van de tekening laat het eeuwenoude patroon zien, zie onderstaande foto. De onregelmatige negenhoeken, paarsgewijs getekend in de strikvormige girihtegels, zijn goed herkenbaar.
Op de onderste helft is mijn nieuwe constructie van een ander patroon te zien waarbij ik in plaats van negenhoeken kleinere vijfpuntige sterren heb geconstrueerd, omringd door zeshoeken.


p.41 Het Kashankleedje gecombineerd met een mozaïek uit Cairo

De bovenste helft toont het mozaïek dat ik, voordat we op reis gingen, had bedacht als variant op het mozaïek op de onderste helft van de tekening die o.a. in Cairo is te bewonderen.
Van de drievoudige 'svastika's' in het midden van elke gestippelde driehoek stapte ik over op viervoudige svastika's in elk gestippeld vierkant. Beide patronen hebben slechts één tegelvorm. Om de overgang van orthogonaal naar isometrisch te realiseren heb ik twee 'koppeltegels' ontworpen.
Wie goed kijkt, ziet dat er nog een klein verschil is tussen het patroon dat ik ontwierp en dat op het kleedje (zie hieronder).
In het kleedje is nog een extra 'draai' aangebracht bij de swastika's. Net als bij de meeste andere patronen kent de basisvorm vele varianten.
Wat bij het kleedje opvalt is, dat de boven-en onderrand van het mozaïek precies op symmetrielijnen liggen, maar dat dit niet het geval is aan de linker- en rechterrand. Dit wordt in de ontwerppraktijk veelal gezien als een 'fout'; het mozaïek past niet mooi in het 'frame', zie de discussie hierover op p.60


p.49 Het patroon met zevenhoeken in de Vrijdagmoskee, Isfahan

Dit patroon (zie hierboven) is voor mij één van de meest fascinerende patronen die ik ooit gezien heb. Dit komt ook doordat het niet eens zozeer opvalt omdat het in de afgelegen Noordkoepel van de Vrijdagmoskee in Isfahan is uitgevoerd als een reliëf, zonder kleuren, en ook nog eens een paar meter boven ooghoogte is aangebracht. Dit verhoogt het mysterie rond dit patroon, dat in de 11e eeuw na Christus moet zijn ontworpen, vermoedelijk door Omar Khayám zelf, en al het rumoer van de daaropvolgende eeuwen, inclusief meerdere restauraties, zo vermoed ik, goed doorstaan heeft.
Het meetkundig interessante is, dat er perfect regelmatige zevenhoeken in voorkomen. Twee ervan zie je in het midden van het paneel, twee midden-boven, en twee halve midden-onder.


In de tekening hierboven is te zien dat het patroon is afgeleid van een raster van twee soorten zeshoeken. Dit raster is een op een slimme manier vervormde honingraat. De hoeken van deze honingraat zijn zo gekozen, dat rondom bepaalde driesprongen regelmatige zevenhoeken kunnen worden getekend.
Professor J.P. Hogendijk ontdekte in de jaren nul iets opmerkelijks: In een manuscript uit rond 1600 staat een constructie van precies dit patroon, zie de foto hieronder. Dit manuscript bevindt zich in Parijs. Het bijzondere van dit manuscript is, dat er behalve een tekening (van de hierboven gestippelde rechthoek) ook een aantal instructies zijn genoteerd over hoe het patroon moet worden getekend. Dit is zeer uitzonderlijk. Een geoefend meetkundige kan met behulp van deze instructies het patroon exact reproduceren op een zelfgekozen schaal.
Dit alles tesamen heeft me geïnspireerd om nader onder zoek te doen naar patronen die zevenvoudige symmetrie herbergen


p.57 Het 'patroon uit Mosul'

Dit patroon met regelmatige zevenpuntige sterren kwam ik tegen in een boek met tekeningen, gemaakt door Bourgoin, een Fransman die eind 19e eeuw in het Midden-Oosten studie maakte van tientallen mozaïeken en hierover publiceerde. Later vond ik het in een boek van Eric Broug, die het in verband bracht met een tableau op de Imam Yahyah moskee in Mosul. Dit blijkt echter niet correct te zijn (zie p. 108 van Snijpunt Isfahan), waarover verderop meer.
In de tekening boven is te zien dat er een vierkant raster is gebruikt. Binnen elk vierkant zijn tweetallen gekantelde kruizen getekend. De kantelhoek is zo gekozen, dat er lokale zevenvoudige symmetrieën worden gecreëerd rondom punten die op de lijnen van het vierkante raster liggen. Deze punten vormen de centra van de zevensterren.
De ontwerper van het patroon heeft vervolgens een creatieve keuze gemaakt. In tegenstelling tot de standaard-ontwerpmethode koos hij ervoor om bij elke zevenster de lijntjes die samenkomen in twee sterpunten niet te verlengen. Hierdoor ontstaan in het totaalpatroon gekantelde vierkanten met op elk van de vier zijden een 'inham'. Bekijk je een groot stuk van het patroon, dan zijn er als het ware golvende vierkanten te zien. In de middens van deze vierkanten zijn regelmatige achthoeken geconstrueerd.
De klaver-drie-vormen zijn niet perfect drievoudig symmetrisch, maar dit valt nauwelijks op. Het ontwerp blinkt uit in eenvoud, gecombineerd met raffinement. De ontwerper -niemand weet wie zij of hij was- moet in het bezit zijn geweest van grote kennis van meetkunde, gecombineerd met een fikse dosis creativiteit.
Op een zeker moment tijdens mijn studies van dit patroon, en van andere, kwam ik op het idee om de vondst van de gekantelde kruisende lijnen toe te passen in een isometrisch raster. Met dit idee ging ik aan de slag, in eerste instantie vond ik een nieuw patroon met zevensterren waar ik zo enthousiast mee de huiskamer instormde (p.15). Later maakte ik een verbeterde variant van dit ontwerp (dit was niet lang voor ons vertrek naar Isfahan) en dat is maar goed ook, want het eerste ontwerp bevatte één tegelvorm die binnen de ontwerptraditie op zijn zachtst gezegd nogal dubieus is. De verbeterde versie staat op de omslag en op p.17 van Snijpunt Isfahan. Hiermee togen we naar het Mekka van de ontwerptraditie.
p.82 Het patroon op de minbar van de moskee van Varzane


In dit ontwerp is een aantal a-typische keuzen gemaakt. Misschien is het wel geconstrueerd door een leerling-ontwerper die enkele 'ontwerpregels' overtrad, maar het toch mocht uitvoeren, helemaal onderaan de minbar, bij wijze van ludieke toevoeging.
Het meest opvallende element is een achtpuntige ster, op een grid van vierkanten. Opmerkelijk is, dat in de sommige van deze sterren kleine vierkantjes zijn getekend, en in andere sterren met een svastika een vierdeling is gemaakt. Die laatste keuze breekt de spiegelsymmetrie van het patroon maar vergroot de levendigheid.
De vliegers rondom de achtsterren sluiten aan op regelmatige zeshoeken op een wijze die ik nergens elders zag. In het ontwerp zijn verder regelmatige achthoeken en vierkantjes verwerkt.
Ik zag dit patroon tijdens mijn eerste bezoek aan Iran in 2010 tijdens een doldwaze reis waarin Tom Goris mij in negen dagen meenam naar een duizelingwekkend aantal locaties met fascinerende tableaus.
Destijds was de minbar nog niet ingepakt, maar wel al in slechte staat. Hopelijk wordt de minbar ooit gerestaureerd.
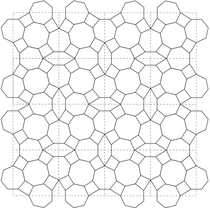
p.107 Het mozaïek dat ik in een plastic zakje van Mr. Ghanbari kreeg

Dit patroon met tienvoudige symmetrie is alom bekend in de islamitische wereld, met name in de Perzische en Ottomaanse regio's.
Linksboven zijn alle spiegel-symmetrieën, inclusief de lokale symmetrieën, aangegeven met stippellijnen.
Rechtsboven zijn met dunne lijnen delen van girihtegels herkenbaar: Regelmatige tienhoeken, gecombineerd met strikvormen.
Rechtsonder is een andere verdeling met girihtegels te zien: Kleinere tienhoeken gecombineerd met 'geplette' zeshoeken en regelmatige vijfhoeken.
De keuze voor hetzij de bovenste, hetzij de onderste verdeling is tamelijk willekeurig.
De grote gestippelde rechthoek linksonder is precies ook de opbouw van het kleine tableau dat ik van Mr. Ghanbari kreeg, in de kleuren okergeel, bruin, wit, donkerblauw en turquoise.
Onderstaande foto's laten zien hoe ik de mozaïeksteentjes met specie samenbracht tot een tableau.



p. 109 Een correcte reconstructie van het reliëf uit Mosul
In de verantwoording van Snijpunt Isfahan staat dat het 'Patroon uit Mosul' geen orthogonaal, maar een isometrisch grid heeft. Hierbij een toelichting.

Dit is een reconstructie van het patroon dat op het grote tableau was aangebracht op een zijmuur van de Imam Yahyah moskee in Mosul dat door IS is verwoest.
In het mozaïek zijn, net als in het patroon van p.57, onder elkaar, gekantelde vierkanten te zien waartussen zevenpuntige sterren als het ware zijn ingeklemd.
Er is echter een opmerkelijk verschil. Wie goed kijkt ziet, dat er zich uiterst linksboven en rechtsonder kwarten van zespuntige, en niet zevenpuntige sterren bevinden. Ook zijn er links en rechts halve zespuntige sterren te zien. Zespuntige sterren komen in het patroon van p.57 niet voor.
Wat blijkt?: Het patroon heeft een grid, bestaande uit rechthoekige driehoeken die paarsgewijs gelijkzijdige driehoeken vormen. Het grid is dus isometrisch en niet vierkant.
Het patroon heeft wel heel andere symmetrieën dan mijn ontwerp; Zesvoudige in plaats van drievoudige draaisymmetrie, en loodrecht op elkaar staande symmetrielijnen.
Uiteindelijk ben ik blij met het feit dat Eric Broug niet volledig was met zijn analyse van het tableau (p.175 van zijn mooie boek 'Islamic Geometric Design' Uitgeverij Thames & Hudson) want mede hierdoor heb ik mijn nieuwe ontwerp gevonden. Op de onderste helft van de tekening is een cirkel te zien die verdeeld is in 84 gelijke delen. hiermee kan het ontwerp geconstrueerd worden, zo vond ik in de winter van 2022.
Hieronder een andere constructietekening die ik in 2017 maakte van één driehoek uit het Imam Yahyah tableau waarmee het gehele patroon kan worden opgebouwd. Het ontwerp is fascinerend omdat het onmogelijk is om tegelijkertijd perfecte vierkanten en regelmatige zevensterren in het patroon te verwerken. Er zijn concessies nodig. Overigens heeft Jay Bonner zich in zijn magnum opus niet gewaagd aan dit patroon...


Tenslotte, het Tableau waar het allemaal om draaide...
Heb je het boek gelezen en ben je benieuwd naar het eindresultaat?
Klik dan HIER
 José Goossen Karssenberg Islamitische Meetkundige Patronen
José Goossen Karssenberg Islamitische Meetkundige Patronen